Thermal Demo-Aluminum Bar

Case content

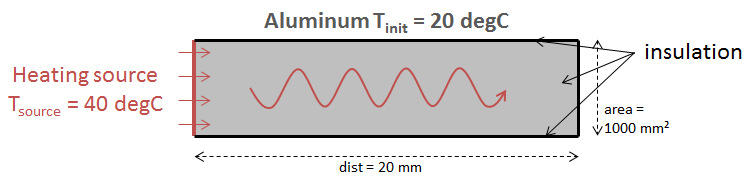
This case introduces a Demo case in the Simcenter Amesim Thermal library, namely the heat conduction of an aluminum plate.

Case content: The heat conduction model of an aluminum plate. A constant temperature of 40 degrees is applied to the left side, and the upper and lower surfaces of the aluminum plate are insulated. The temperature rise characteristics of the aluminum plate are to be obtained.

This case is relatively simple. You can learn this case directly by reading my article, and there is no need to look through the help document again. The official case is as follows

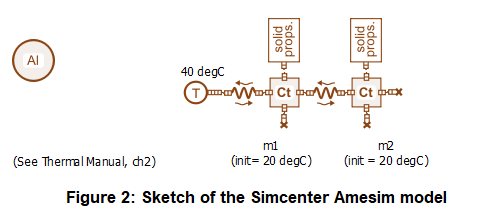
First, analyze several problems that beginners may encounter

Question 1

Why does an aluminum block need to be modeled with two heat capacity components THC000? Actually, one can also be used. Dividing it into two is equivalent to discretizing the aluminum block into two parts, and it can also be discretized into multiple parts. The more the number of discretizations, the more precisely the temperature of the aluminum block can be calculated, and the higher the accuracy.

Question 2

After dividing into two heat capacities, that is, dividing the aluminum block into two sections of 10mm each. Each heat capacity element represents one section, and each heat capacity element has 4 interfaces. So, is the temperature calculated by the software the average temperature of this 10mm section? The highest temperature? Or which temperature?

By referring to the help document of THC000, a very crucial sentence was found, that is, the temperatures of the 4 ports are the same. This indicates that the temperature of the heat capacity element calculated refers to the average temperature of this element.

t1 = t2 = t3 = t4 = T

So if a 20mm aluminum block is divided into 100 parts, it is equivalent to knowing the temperatures of 100 consecutive points along the 20mm length, which provides higher accuracy. However, generally two segments are sufficient. This can also explain why Amesim discretizes it into two parts. Since what is calculated is the average temperature, if an aluminum block is very large, using only one average temperature to represent its temperature characteristics is not very accurate. Therefore, it is divided into two parts, and the average temperature of each part is calculated separately, with a slightly higher perspective.

Points that are easy to fall into traps 1

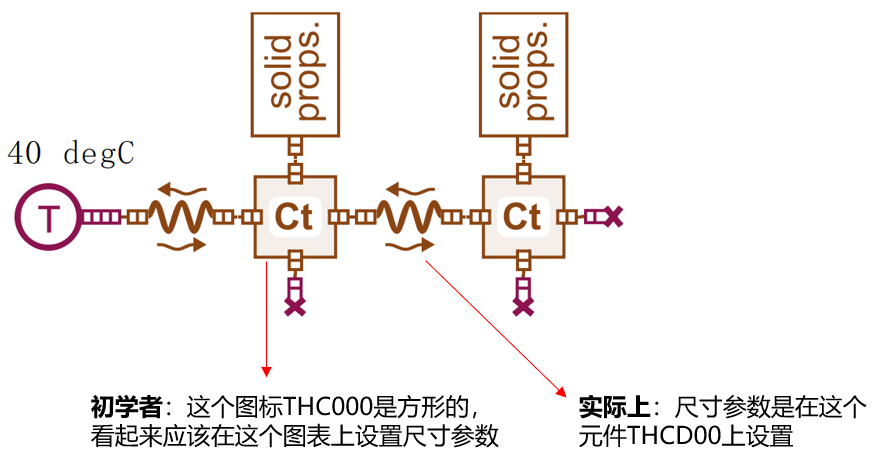
Misunderstandings Caused by Icon Shapes

When beginners first look at this case, it is easy to have an illusion through the icons. The square icons look square and seem to imply aluminum blocks. Naturally, one would think that the size parameters of the aluminum blocks should be set on them, but this is not the case.

In fact, they are set on the component that looks like a heat-conducting element.

The heat capacity component THC000, which seems to be related to the shape, is only used to represent volume and is a capacitive component.

The heat-conducting component THCD00, which seems to have nothing to do with the shape, is used to express the shape and various sizes can be set.

Points that are easy to fall into traps 2

THCD00 can represent two shapes :

• regular shapes: linear (linear case) and hollow cylinder.

• Any irregular shape: represented by the shape factor sf (shape factor). The help provides the sf calculation formulas for simple irregular shapes such as hollow square tubes. For more content, please refer to the reference [1] F. P. INCROPERA, D. P. DEWITT: "Fundamentals of Heat and Mass Transfer", Fourth Edition, John Wiley & Sons Inc, 1996.

Here comes the second pitfall. Combining the aluminum block in the case with the linear shape (linear case), it's easy to misunderstand the linear case as a flat plate. It should be noted that "linear" doesn't necessarily mean a flat plate.

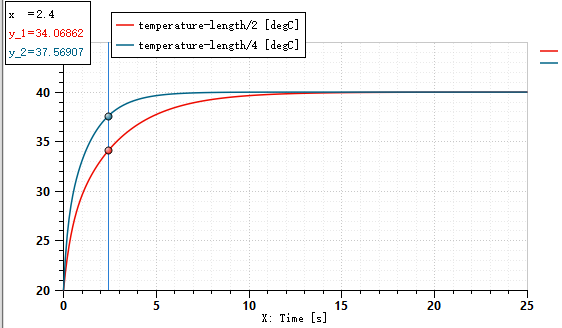
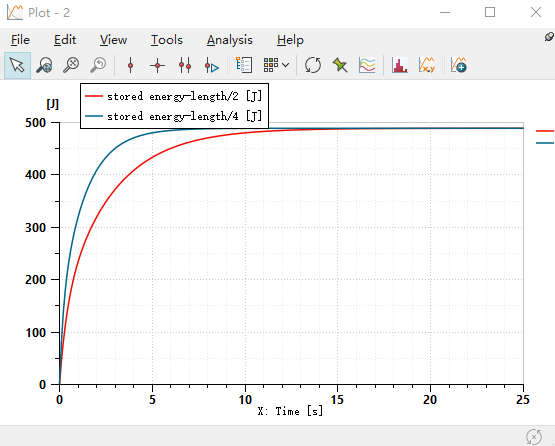
Even if area*length/2 is numerically equal to the volume of half of the aluminum block, it's just a numerical equality, and it may not have much physical significance. Let's verify this. Change the distance to length/2 and length/4 respectively (length is a global parameter representing the length of the aluminum block), and keep other settings unchanged for calculation. It is found that the temperature rise rate of length/4 is indeed faster, but the heat stored in the two sections of the aluminum block remains the same in the end. This proves that distance only affects the heat transfer rate, and the heat stored in the end is only related to the volume set in the heat capacity element.

Upon further analysis, in the linear case, "area" represents the cross - sectional area in the direction perpendicular to the heat conduction direction, which is used to measure the effective area involved in heat conduction. "distance1" represents the distance between two points in the heat conduction direction, reflecting the length of the heat conduction path. They are mainly used to calculate the heat flux rate, which has a different role in heat conduction compared to the concept of volume. In the formula for calculating the heat flux rate in the linear case,

$$dh1=\frac{\lambda_{1} \cdot area }{ distance 1}(t2 - t1)$$

The formula focuses on the heat conduction through a specific cross - section ("area") along a certain path ("distance 1"), rather than considering it from the perspective of volume.

In thermology, volume is generally used to calculate the heat capacity and heat - storage capacity of an object. In heat conduction, the combination of "area" and "distance 1" is based on Fourier's law of heat conduction to describe the heat conduction phenomenon. Even if numerically distance 1 multiplied by "area" is equal to volume, in heat conduction calculations, what is concerned is the heat transfer efficiency and flux, which is not the same concept as the volume - related physical processes (such as heat storage).

So this may be the reason why Amesim uses the combination of two components to express the heat conduction of a component. One component describes the size characteristics of the object and calculates the heat conduction phenomenon, and the other heat - capacity component describes the heat - storage process of the object.

Highlights of the case

The upper and lower surfaces of the aluminum block are insulated. In addition to being blocked by thermal plugs, in this case, solid props are also used for blocking. This not only has an insulating effect but also allows for the viewing of other parameters of the aluminum block through it.